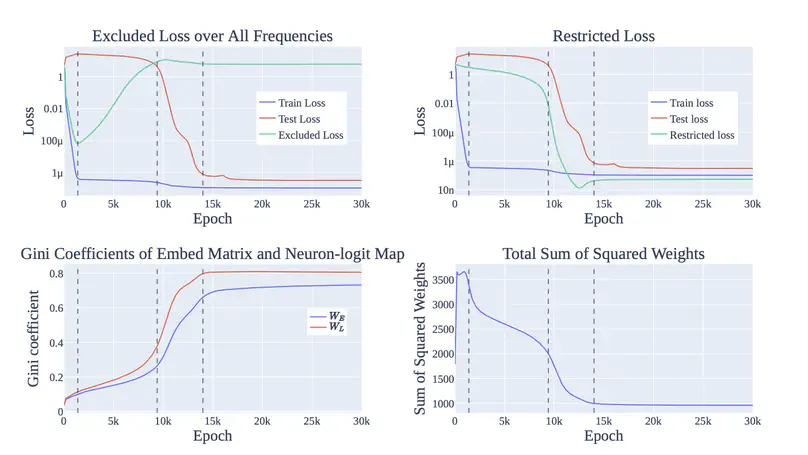
Publications

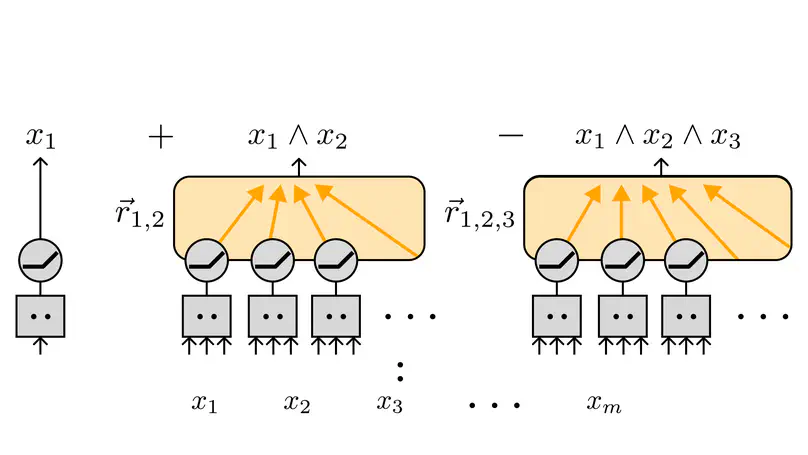
We formally study what sparse circuits neural networks can represent and compute in superposition – that is, using sparse features respresented near-orthogonally in a high-dimensional space. We show that not only can ReLU MLPs perform more computation at a fixed given width by placing features in superposition, but also that they can maintain superposition through multiple layers.

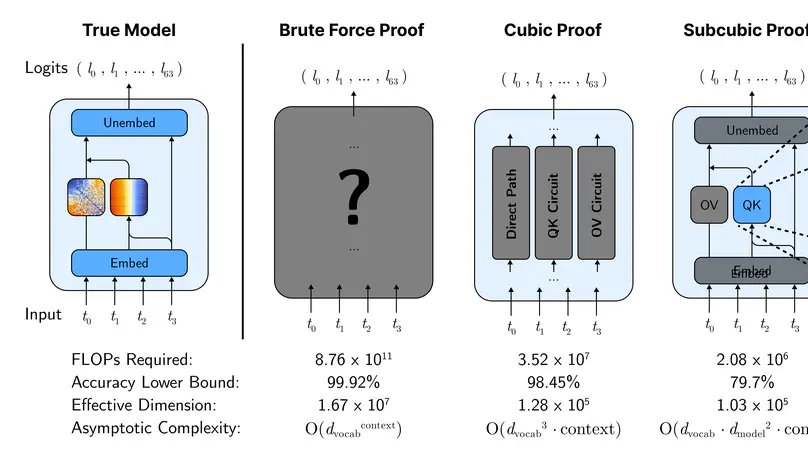
We use mechanistic interpretability to general compact formal guarantees on model performance on a toy Max-of-K task. We find that shorter proofs seem to require more mechanistic understanding and more faithful mechanistic understanding leads to tighter performance bounds. We identify compounding structureless noise as a key challenge for the proofs approach.

We create four agents from Claude and GPT-4 to investigate the ability of frontier language models to perform autonomous replication and adaptation.

We reverse engineer small transformers trained on group composition and use our understanding to explore the universality hypothesis.

We fully reverse engineer 32 small transformers trained on modular addition and use this understanding to study grokking.

We compare humans to small language models on next-token prediction tasks, and find that even relatively small language models consistently outperform humans.

We argue that AGIs trained in similar ways as today’s most capable models could learn to act deceptively to receive higher reward; learn internally-represented goals which generalize beyond their training distributions; and pursue those goals using power-seeking strategies.

We introduce a more principled approach for evaluating the quality of mechanistic interpretations via behavior-preserving resampling ablations—converting hypotheses into classes of activations inside a neural network can be resampled without affecting behavior.

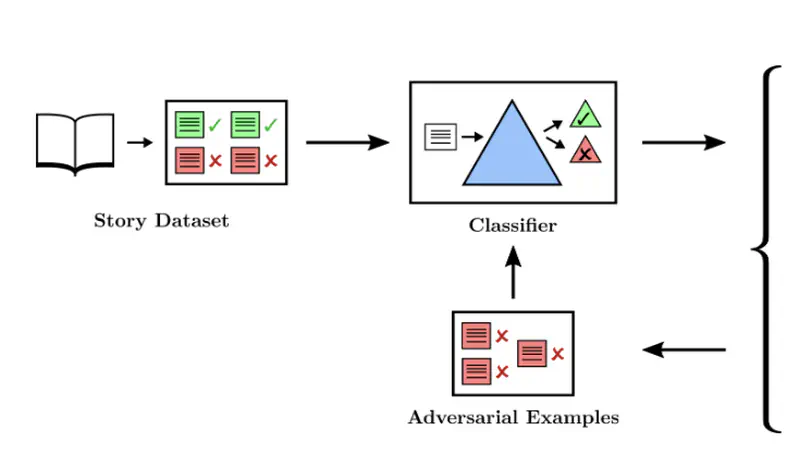
We study the limits of adversarial training on a injury classification task using a variety of attacks including a new saliency map–based snippet rewrite tool to assist our human adversaries. While advesarial training was not able to eliminate all in-distribution failures, it did increase robustness to the adversarial attacks that we trained on.

We study the effect of human irrationality on reward inference. We find that irrationality can both help and hurt reward inference, depending on the type of irrationality. We also find that the effect of irrationality on reward inference is not monotonic in the degree of irrationality.

We illustrate the benefits of agents that try to assist humans, over agents that learn a reward during training and then maximize said reward after deployment.

We study the problem of learning to assist a human who is themselves learning about their preferences.